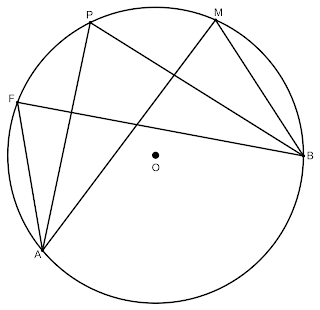
Ъгъл чийто връх е вътрешна точка за окръжност. Ъгъл чийто връх е външна точка за окръжност 8 клас
.png)
Теорема 1 Ъгъл чийто връх е вътрешна точка на една окръжност, се измерва с полусбора от мерките на дъгите, заключени между раменете му, и техните продължения. $\sphericalangle AED=\frac{\overset{\frown}{AD}+\overset{\frown}{BC}}{2}$. Теорема 2 Ъгъл, чийто връх е външен за една окръжност, а раменете му имат общи точки с тази окръжност, се измерва с полуразликата от дъгите, заключени между раменете му. На горната фигура виждаме различните възможности, които може да имаме за ъгъл чийто връх е външен за една окръжност, а раменете му имат общи точки с окръжността. Ъглите от фигурата на равни съответно на: $\sphericalangle MLN=\frac{\overset{\frown}{MN}-\overset{\frown}{PQ}}{2}$, $\sphericalangle MLQ=\frac{\overset{\frown}{MQ}-\overset{\frown}{PQ}}{2}$ и $\sphericalangle MLQ=\frac{\overset{\frown}{MRQ}-\overset{\frown}{MQ}}{2}$. 1 Задача Хордите $AB$ и $AC$ в окръжност $k$ са равни и образуват ъгъл $50^{\circ}$. Допирателната към $k$ в точка $B$ пресича правата $AC$ в точка $M$. Намерете ...