Окръжност. Взаимно положение на окръжност и точка и окръжност и права. Допирателна към окръжност 8 клас
1. Основни понятия
Окръжност $k$ с център $O$ и радиус $r$ ще означаваме по следният начин - $k(O;r)$.
.png "окръжност, основни понятия")
$O$ - център на окръжността;
$AB=2r$;
$OA=OB=OC=r$ - радиуси на окръжността;
${KE}$- хорда;
$\overset{\frown}{KE}$ - дъга принадлежаща на хордата $KE$.
2. Окръжност и точка
1) Точката $B$ лежи на окръжността $k(O;r)$, тогава и само тогава, когато $OB=r$;
2) Точката $A$ е вътрешна за окръжността $k(O;r)$, тогава и само тогава, когато $OA<r$;
3) Точката $C$ е външна за окръжността $k(O;r)$, тогава и само тогава, когато $OC>r$;
4) Ако точките $L$ и $N$ са съответно вътрешна и външна за окръжност $k$, отсечката $LN$ има точно една обща точка $F$ с окръжността $k$.
3. Окръжност и права
Преди да разгледаме различните случаи на взаимното положение на окръжност и права нека припомним, че разстояние от точка до права е перпендикулярът спуснат от точката към правата.
Ако $k(O;r)$ е окръжност, $l$ е права и $M$ е петата на перпендикуляра, спуснат от центъра $O$ към правата $l$, то са възможни следните три случая:
1)
Теорема 2 Дължините на допирателните към дадена окръжност, прекарани през точка вън от окръжността, са равни.
 |
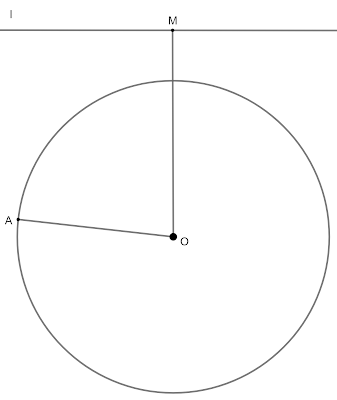| $k$ и $l$ нямат общи точки и $OM>r$ |
2)
 |
| $k$ и $l$ имат две общи точки и $OM<r$ |
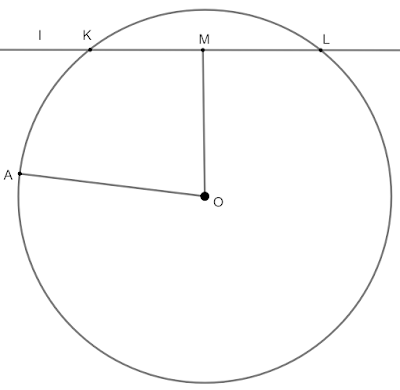
3)
Определение 1 Секуща ще наричаме права, която има две общи точки с окръжността.
 |
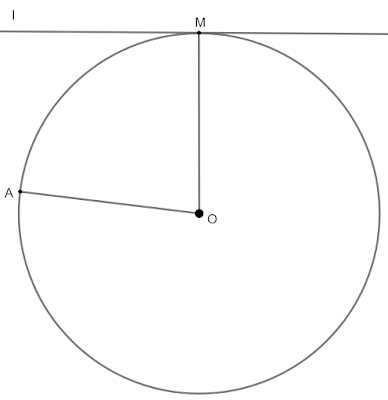| $k$ и $l$ имат една обща точка и $OM=r$ |
Определение 2 Допирателна към окръжността (тангента) ще наричаме права, която има точно една обща точка с окръжността. Тази обща точка ще наричаме допирна точка.
Теорема 1 Ако една права е допирателна на дадена окръжност, тя е перпендикулярна на радиуса в допирната точка.
3. Допирателна от точка към окръжност
Определение 3 Допирателните $t_1$ и $t_2$ към окръжност $k$, които имат обща точка $L$, определят отсечките $LM$ и $LN$, където $M$ и $N$ на съответно допирните точки на $k$ с $t_1$ и $t_2$, които се наричат допирателни от $L$ към $k$.
Доказателство: За доказването на тази теорема ще използваме даденият по-горе чертеж. Тъй като $OM=ON$, $OL$ е обща страна за $\triangle OLM$ и $\triangle OLN$, които са правоъгълни триъгълници (радиусите $OM$ и $ON$ са перпендикулярни на допирателните $t_1$ и $t_2$), следва че те са еднакви по $IV$-ти признак от където получаваме и, че $LM=LN$ (съответните страни и ъгли в еднаквите триъгълници са равни, повече за първи и втори признак за еднаквост може да прочетете тук, за трети признак тук и за четвърти тук).
Следствие 1 Ако през точка $L$, вън от окръжност $k(O;r)$ са прекарани двете допирателни $t_1$ и $t_2$, лъчът $OL^{\rightarrow}$ е ъглополовяща на ъгъла, образуван от допирателните.
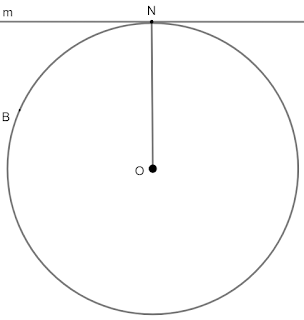
1 Задача Дадени са окръжност $k(O;r=6 \ cm)$ и права $m$. Определете взаимното положение на окръжността $k$ и правата $m$, ако разстоянието от $O$ до правата $m$ е:
а) $6 \ cm$; б) $5 \ cm$; в) $7 \ cm$.
Решение:
а) Тъй като разстоянието от точка до права е перпендикулярът спуснат от точката към правата, в този случай $ON=6 \ cm$ (по условие) и $r=6 \ cm$ следва, че $ON=r=6 \ cm$ и от 3) на трета точка можем да кажем, че правата $m$ е допирателна към окръжността $k(O;r=6 \ cm)$ и точката $N$ е допирна точка, т.е. $k$ и $m$ имат една обща точка.
б) Тъй като разстоянието от точка $O$ до правата $m$ е $ON=5 \ cm$ следва, че $ON<r$ и от 2) на трета точка имаме, че правата $m$ и окръжността $k$ имат две общи точки.
в) Тъй като разстоянието от точката $O$ до правата $m$ е $ON=7 \ cm$ и $ON>r$, от 1) на трета точка следва, че правата $m$ и окръжността $k$ нямат общи точки.
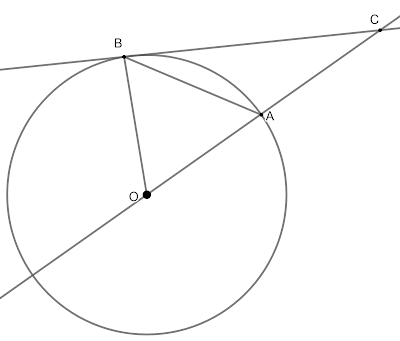
2 Задача Дадени са окръжност $k(O;r)$ и хорда $AB=r$. Върху правата $OA$ е взета точка $C$ така, че $AO=AC$. Докажете, че правата $BC$ е допирателна към окръжността.
Решение:
Ще докажем, че $OBC$ е правоъгълен триъгълник и $OB\perp BC$.
Тъй като $OA=AC$ следва, че точката $A$ е среда на $OC$ и $BA$ е медиана, от където имаме, че $OA=AB=AC=OB=r$ и следователно $\triangle OAB$ е равностранен. Тогава $\sphericalangle OAB=\sphericalangle OBA=\sphericalangle BOA=\sphericalangle 60^{\circ}$. Освен това от факта, че $\sphericalangle BAC=120^{\circ}$ (съседен на $\sphericalangle OAB=60^{\circ}$) и от това, че $\triangle BAC$ е равнобедрен следва, че $\sphericalangle ABC=\sphericalangle ACB=30^{\circ}$ и от тук намираме, че $\sphericalangle OBC=60^{\circ}+30^{\circ}=90^{\circ}$.
3 Задача Точките $A$ и $B$ лежат на окръжност $k(O;r=9 \ cm)$ и $OA\perp OB$. Допирателните към окръжността в точките $A$ и $B$ се пресичат в точка $C$. Докажете, че четириъгълника $OBCA$ е квадрат, и намерете периметъра му.
Решение:
Нека $n$ и $m$ са допирателните към към окръжността $k$ съответно в точките $A$ и $B$. Следователно $OA\perp n$ и $OB\perp m$., т.е. $\sphericalangle OAC=\sphericalangle OBC=90^{\circ}$. Освен това $OA\perp OB$ (по условие) и $\sphericalangle AOB=90^{\circ}$. Така получаваме, че три от ъглите в четириъгълника $OBCA$ са равни на $90^{\circ}$ и тъй като сборът на ъглите в четириъгълник е $360^{\circ}$ следва, че $\sphericalangle ACB=90^{\circ}$. От казаното до тук имаме, че $OBCA$ е правоъгълник, но от това, че $OB=OA=r$ следва, че имаме правоъгълник с равни съседни страни, което означава, че $OBCA$ е квадрат.
4 Задача През точките $A$ и $B$ от окръжност $k(O;r)$ са построени допиратeлни към $k$, които се пресичат в точката $P$. Ако $\sphericalangle AOB:\sphericalangle APB=8:4$ и $OP=16 \ cm$ намерете $r$.
Решение:
Построяваме $OP$. От Теорема 2 знаем, че $\triangle OPA\cong\triangle OBP$ по четвърти признак и следователно $\sphericalangle AOP=\sphericalangle BOP$ и $\sphericalangle APO=\sphericalangle OPB$.
Нека $\sphericalangle AOB=8x$, а $\sphericalangle APB=4x$. От тук следва, че $\sphericalangle AOP=\sphericalangle BOP=4x$, а $\sphericalangle APO=\sphericalangle OPB=2x$. Тогава от теоремата за сбор на ъгли в триъгълник за правоъгълния $\triangle OAP$ следва, че $2x+4x+90^{\circ}=180^{\circ}$, от където $6x=90^{\circ}$ и $x=15^{\circ}$. Така $\sphericalangle AOB=\sphericalangle BOP=60^{\circ}$, $\sphericalangle APO=\sphericalangle BPO=30^{\circ}$. Тъй като от правоъгълния $\triangle OPA$ имаме остър ъгъл от $30^{\circ}$, то от теоремата за катет срещу остър ъгъл от $30^{\circ}$ в правоъгълен триъгълник получаваме, че $AO=\frac{1}{2}OB$ от където $AO=r=8 \ cm$.
5 Задача Правата $AB$ има една обща точка $H$ с окръжност с център $O$ и радиус $6 \ cm$. Ако $\sphericalangle AOB=90^{\circ}$ и $AO=BO$, намерете лицето на $\triangle ABO$.
Решение:
.png "уроци по математика за 8 клас")
6 Задача Даден е квадрат $ABCD$ с пресечна точка на диагоналите $O$ и страна с дължина $6\sqrt{3} \ cm$. Построена е окръжност $k(O;r)$. Определете броя на общите точки на окръжността $k$ и правата $AB$, ако:
а) $r=2\sqrt{6} \ cm$; б) $r=\sqrt{27} \ cm$; в) $r=4\sqrt{2}$ cm.
Решение:
а) За да можем да преценим взаимното положение на окръжността $k$ и правата $AB$ трябва да сравним разстоянието от центъра на окръжността $k$ до правата $AB$ и радиуса на окръжността $k$. За целта намираме $OH$. Тъй като триъгълникът $AHO$ е равнобедрен правоъгълен триъгълник то $AH=OH=3\sqrt{3} \ cm$ ($OH$ е височина, медиана и ъглополовяща в $\triangle ABO$ от където $\sphericalangle AOH=\sphericalangle HAO=45^{\circ}$ и $AH=ON=\frac{1}{2}AB$ повече за квадрата и свойствата му може да намерите тук). Сега като вземем в предвид, че $OH=3\sqrt{3}>r=2\sqrt{6} \ cm$ следва, че окръжността $k(O;r=2\sqrt{6} \ cm)$ и правата $AB$ Нямат общи точки.
б) Тай като $OH=3\sqrt{3} \ cm$ и $r=\sqrt{27} \ cm$ следва, че $OH=r=3\sqrt{3} \ cm$. Така можем да кажем, че правата $AB$ и окръжността $k$ имат една обща точка $H$ и правата $AB$ е допирателна към окръжността $k$.
в) Тъй като $OH=3\sqrt{3} \ cm$ и $r=4\sqrt{2} \ cm$ следва, че $OH<r$ и окръжността $k$ и правата $AB$ имат две общи точки.
Задачи за самостоятелна работа:
1. Допирателната към окръжност в точка $B$ пресича права, минаваща през центъра $O$ на окръжността, в точка $A$. Ако $\sphericalangle AOB=60^{\circ}$ и $AO=8 \ cm$, намерете радиуса на окръжността.
2. През точка $M$, външна за окръжност, са построени допирателните $MP$ и $MR$. Ако разстоянието от $M$ до $R$ е $4 \ cm$, намерете дължината на допирателната отсечка $MR$.
3. Даден е равнобедрен $\triangle ABC$ с $\sphericalangle ACB=120^{\circ}$. С център средата $M$ на страната $AB$ е построена окръжност, която се допира до $AC$ и $BC$. Ако радиусът на окръжността е $5 \ cm$ и $MC=p \ cm$, намерете лицето на $\triangle ABC$.
4. За $\triangle ABC$ ($\sphericalangle C=90^{\circ}$) е известно, че $AB=9 \ cm$ и $\sphericalangle A=60^{\circ}$. Окръжност $k(A,r)$ се допира до правата $BC$. Намерете радиуса на тази окръжност.
5. Дадена е отсечка $AB=8 dm$. Построена е симетралата $s$ на тази отсечка и окръжност $k(B;r=40 \ cm)$. Определете взаимното положение на $k$ и $s$.
Още решени и обяснени задачи може да намерите във видеото ми по-долу:
Коментари
Публикуване на коментар