Релации - основни понятия и дефиниции
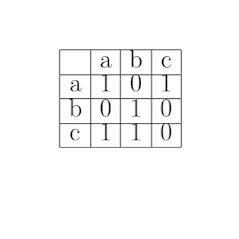
Определение 1: Нека $n$ е естествено число и $M_1, M_2,\ldots M_n$ e фамилия от множества. Всяко подмножество $R\subseteq M_1\times M_2\times\ldots\times M_n$ се нарича $n$-местна релация, а множествата $M_1, M_2,\ldots M_n$ се наричат първи, втори и т.н. $n$-ти домен на тази релация. Ако вземем $n=2$ получената релация се нарича двуместна или още бинарна релация. Ако $(m,n)\in R$, където $R$ е бинарна релация ще използваме инфиксният запис $mRn$. Така от дефиницията ясно се вижда, че ако елементите на едно множество $M$ са в релация с елементите на друго множество $N$ естествено се поражда множеството $M\times N$, което определя дадената релация. Съществуват два начина на задаване на релации - конструктивно и дескриптивно . Нека да разгледаме следващият пример. Пример 1: Нека имаме множествата $M=\{10,20,30,40\}$ и $N=\{4,5\}$. Разглеждаме следните две бинарни релации, които са зададени дескриптивно: $R_1=\{(m,n)| m\in M, n\in N,\ m\ се\ дели\ на\ n\}$ и $R_2=\{(m,n)...