Медицентър на триъгълник 8 клас
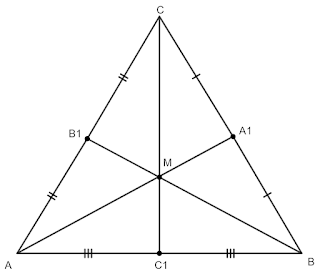
Определение 1: Пресечната точка на трите медиани на триъгълник се нарича медицентър на триъгълника.
Теорема 1: Трите медиани на триъгълник се пресичат в една точка, която дели всяка от тях в отношение $2:1$, считано от съответния връх на триъгълника.
Като коментар към тази теорема можем да кажем, че:
$AM:MA_1=2:1$; $BM:MB_1=2:1$ и $CM:MC_1=2:1$.
Основна задача 1: Нека $M$ е медицентър на $\triangle ABC$, тогава $S_{\triangle ABM}=S_{\triangle BCM}=S_{\triangle CAM}$.
Основна задача 2: Нека $M$ е медицентърът на $\triangle ABC$ и $O$ е произволна точка от равнината, тогава е в сила равенството $\vec{OM}=\frac{1}{3}(\vec{OA}+\vec{OB}+\vec{OC})$.
Нека също така да припомним е едно друго свойство на медианата, което е изучавано през годините, а именно, че всяка медиана на триъгълник го разделя на два равнолицеви триъгълника.
Сега нека да разгледаме някои задачи.
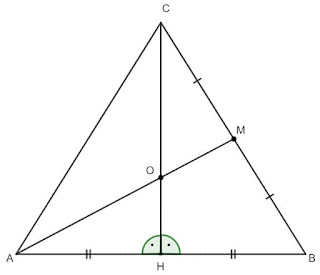
1 Задача: Медианата $AM$ и височината $CH$ на равнобедрения $\triangle ABC$ ($AC=BC$) се пресичат в точка $O$. Ако $S_{\triangle ABC}48$ $cm^2$ и $AB=8$ $cm$, намерете дължината на $CO$.
Решение:
Тъй като $\triangle ABC$ е равнобедрен следва, че $CH$ е височина, медиана и ъглополовяща в триъгълника $ABC$. От тук можем да кажем, че точката $O$ е медицентър и следователно $AO:OM=2:1$, както и $CO:OH=2:1$. За лицето на $\triangle ABC$ имаме, че $S_{\triangle ABC}=\frac{AB.CH}{2}\implies 48=\frac{8.CH}{2}\implies CH=12\ cm.$ Тъй като $CO=2x$, а $OH=x\implies 2x+x=12\implies 3x=12$ и $x=4$, а $CO=2x=2.4=8$ $cm$.
2 Задача В успоредника $ABCD$ точка $E$ е среда на $AD$. Диагоналът $AC$ и отсечката $BE$ се пресичат в точка $P$. Ако $EP=1,3$ $cm$ и $AP=2,2$ $cm$, то намерете дължините на $AC$ и $BE$.
Решение:
Построяваме диагонала $BD$. Нека $AC\cap BD=O$. Тъй като точката $O$ е среда на $BD$ (това е свойство на успоредника) следва, че $AO$ е медиана в $\triangle ABD$. Освен това, тъй като точката $E$ е среда на $AD$ следва, че $BE$ също е медиана в $\triangle ABD$ от където имаме, че точката $P$ се явява медицентър на $\triangle ABD$. Тогава като приложим Теорема 1 от днешният урок получаваме, че $AP:PO=2:1$ и $BP:PE=2:1$. Нека $PO=x$, тогава $AP=2x$ и $2x=2,2\implies x=1,1$ $cm$ т.е. $PO=1,1$ $cm$. Сега тъй като $AC=2AO=2(AP+PO)\implies$ $AC=2(2,2+1,1)=6,6$ $cm$. За да намерим $BE$ вземаме в предвид, че $BE=BP+PE$. Нека $PE=y$ и $BP=2y$. Тъй като $PE=y=1,3$ $cm$ $\implies BP=2.1,3=2,6$. Тогава $BE=1,3+2,6=3,9$ $cm$.
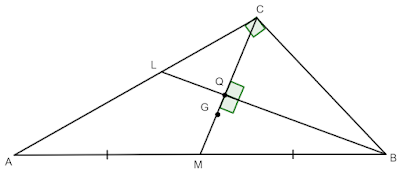
3 Задача Даден е правоъгълният $\triangle ABC$ с прав ъгъл при върха $C$. Ъглополовящата $BL$ е перпендикулярна на медианата $CM$ и я пресича в точка $Q$. Ако $AB=42$ $cm$ и точка $G$ е медицентър на $\triangle ABC$, намерете дължината на отсечката $QG$.
Решение:
Тъй като $BQ\perp CM$ (по условие) и $BQ$ е ъглополовящата на $\sphericalangle ABC\implies \triangle MBC$ е равнобедрен и $MB=BC$. Също така и $MQ=CQ$ (BQ е медиана). Но $CM$ е медиана към хипотенузата в правоъгълният триъгълник $ABC$ следователно $CM=AM=MB$ от където имаме, и че $MB=BC=MC$ и така получаваме, че $\triangle MBC$ е равностранен. От тук следва, че $\sphericalangle CMB=\sphericalangle MBC=\sphericalangle MCB=60^{\circ}$ и $\sphericalangle BAC=\sphericalangle MBQ=\sphericalangle CBQ=30^{\circ}$. От правоъгълният триъгълник $MBQ$, като приложим теоремата за остър ъгъл от $30^{\circ}$ следва, че $MQ=\frac{1}{2}MB$, т.е. $MQ=CQ$. Нека $CM=3x$. Тъй като $CQ=MQ=1,5x$ имаме, че $3x=21$ и $x=7$ $cm$, следователно $GQ\frac{x}{2}=3,5$
Задачи за самостоятелна работа:
1. В триъгълника $ABC$, $CM$ е медиана, като $AB:CM=2:3$. Докажете, че медианите през върховете $A$ и $B$ са перпендикулярни.
2. Даден е успоредник $ABCD$. Докажете, че медицентровете на триъгълниците $ABC$, $BCD$, $CDA$ и $DAB$ са върхове на успоредник.
3. Даден е успоредникът $ABCD$. Точките $E$, $F$, $G$ и $H$ са медицентрове съответно на триъгълниците $ABD$, $ABC$, $BCD$ и $CDA$. Ако $AC=24$ $cm$, $BD=18$ $cm$, намерете дължините на диагоналите на четириъгълника $EFGH$.
4. Да се докаже, че в равнобедрения триъгълник медианите към бедрата са равни. (задачата може да се реши със и без използването на свойството на медицентъра на триъгълника)
5. Даден е триъгълникът $ABC$ и правата $p$, която пресича страните $CA$ и $CB$ на триъгълника $ABC$. Разстоянията от върховете $A$ и $B$ до $p$ са съответно $3$ $cm$ и $5$ $cm$, а разстоянието от медицентъра на триъгълника $ABC$ до правата $p$ е $2$ cm. Да се намери разстоянието от $C$ до правата $p$.
6. В равностранния $\triangle ABC$ е построена височината $CD$ ($D\in AB$). Точките $G_1$ и $G_2$ са медицентрове съответно на $\triangle ADC$ и $\triangle BDC$. Докажете, че периметърът на $\triangle ABC$ е $3$ пъти по-голям от периметъра на $\triangle G_1G_2D$.
Още обяснени и решени задачи може да намерите във видеото ми по-долу:




Коментари
Публикуване на коментар