Уроци по математика (Math lessons)

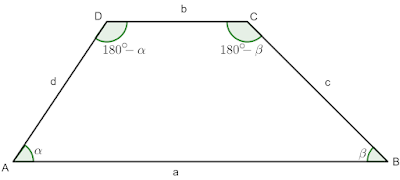
Определение 1: Трапецът е четириъгълник, на който една двойка срещуположни страни са успоредни. На чертежа имаме трапец $ABCD$ в който $AB\parallel CD$, като $AB=a>CD=b$.  $AB$ - голяма основа; $CD$ - малка основа; $AD=d$ и $BC=c$ - бедра За всеки трапец е изпълнени, че $\sphericalangle A+\sphericalangle D=\sphericalangle B+\sphericalangle C=180^{\circ}$, защото двойките ъгли $\sphericalangle A$ и $\sphericalangle D$, както и $\sphericalangle B$ и $\sphericalangle C$ са съответни ъгли и тъй като правите $AB$ и $CD$ са успоредни имат сбор от $180^{\circ}$. По специалните видове трапци са: 1) Правоъгълен трапец Определение 2: Трапец, на който едното бедро е перпендикулярно на основите му се нарича правоъгълен трапец. $ABCD$ - правоъгълен трапец в който $AD\perp AB$ и $AD\perp CD$ и $\sphericalangle A=\sphericalangle D=90^{\circ}$.  Тук $CH$ е височина в трапеца $ABCD$ и $CH=AD$, защото $AHCD$ е правоъгълник. Можем още да кажем, че тъй като $AB=a$, $CD=b$ и от $AH=CD$ следва...

Определение 1: Пресечната точка на трите медиани на триъгълник се нарича медицентър на триъгълника. Теорема 1: Трите медиани на триъгълник се пресичат в една точка, която дели всяка от тях в отношение $2:1$, считано от съответния връх на триъгълника.  Като коментар към тази теорема можем да кажем, че: $AM:MA_1=2:1$; $BM:MB_1=2:1$ и $CM:MC_1=2:1$.   Основна задача 1: Нека $M$ е медицентър на $\triangle ABC$, тогава $S_{\triangle ABM}=S_{\triangle BCM}=S_{\triangle CAM}$. Основна задача 2: Нека $M$ е медицентърът на $\triangle ABC$ и $O$ е произволна точка от равнината, тогава е в сила равенството $\vec{OM}=\frac{1}{3}(\vec{OA}+\vec{OB}+\vec{OC})$. Нека също така да припомним е едно друго свойство на медианата, което е изучавано през годините, а именно, че всяка медиана на триъгълник го разделя на два равнолицеви триъгълника. Сега нека да разгледаме някои задачи.  1 Задача: Медианата $AM$ и височината $CH$ на равнобедрения $\triangle ABC$ ($AC=BC$) се пресичат в точка $...

Както вече знаем в определени задачи имаме дадена аритметична или геометрична прогресия и след като извършим дадени аритметични действия с техните членове получаваме съответно геометрична или аритметична прогресия. Много често се налага търсенето на членовете им, техните суми и т.н. Ето защо за решаването на такъв тип задачи е много важно да знаем всички свойства, както на аритметичната, така и на геометричната прогресия. Нека сега разгледаме някои примери. 1 Задача Числата $a_1$, $a_2$ и $a_3$ образуват намаляваща геометрична прогресия, а числата $a_1$, $a_2+2$ и $a_3$ са последователни членове на аритметична прогресия. Намерете $a_1$, $a_2$ и $a_3$, ако произведението $a_1.a_2.a_3=512$. Решение: За членовете на геометричната прогресия изразени чрез $a_1$ и $q$ имаме, че $a_2=a_1q$, а $a_3=a_1q^2$. Следователно членовете на аритметичната прогресия можем да запишем по следният начин $a_1$, $a_1q+2$, $a_1q^2$. От свойствата на аритметичната прогресия знаме, че всеки среден член е сре...

 Спомняте ли си кои са били първите операции с числа, на които се учехте в училище? Това са събиране и изваждане, които сега вероятно вече ви се виждат толкова елементарни, че сякаш сте ги знаели цял живот. След събирането и изваждането, научаваме и че числата могат да се умножават и съответно делят. Делението, особено на по-големи числа, за повечето от нас си остава трудна задача. Но в неговата сложност се крие и магията.  Ако се захванем да откриваме всички делители на всяко число, ще станем свидетели на много скрити и любопитни закономерности. Да разгледаме делителите на първите няколко числа: $2$ се дели на $1$ и на $2$; $3$ се дели на $1$ и $3$; $4$ се дели на $1$, $2$ и $4$; $5$ се дели на $1$ и $5$; $6$ се дели на $1$, $2$, $3$ и $6$; $7$ се дели на $1$ и $7$; $8$ се дели на $1$, $2$, $4$ и $8$; $9$ се дели на $1$, $3$ и $9$; $10$ се дели на $1$, $2$, $5$ и $10$; $11$ се дели на $1$ и $11$ и т.н.   Прости числа Първото, което ни прави впеч...

Определение 1: Числова редица (основните факти за числовите редици може да намерите тук ), в която всеки член, след първия, се получава, като предходният член се умножи с едно и също число, се нарича геометрична прогресия. Числото, с което се умножава всеки член след първия за да получим следващият се нарича частно на геометричната прогресия и се означава с $q$. С $a_1$ и $a_n$ ще означаваме първият и $n$-тият член (общият член) на геометричната прогресия. Както и при аритметичната прогресия с $n$ ще означаваме броят на членовете на една геометрична прогресия, а с $S_n$ сумата на първите $n$ члена на геометрична прогресия. Една крайна геометрична прогресия е определена, ако знаем $a_1$, $q$ и $n$, докато една безкрайна прогресия е определена, ако знаем само $a_1$ и $q$. Формулата за намиране на $n$-тият член на една геометрична прогресия е $a_n=a_1.q^{n-1}$. Освен това в сила са и следните формули за сумата на първите $n$ члена на една геометрична прогресия $S_n$=\frac{a_1-a_nq}{1-q}...

Определение 1: Числова редица , в която всеки член след първия се получава като към предходния му се прибави едно и също число, се нарича аритметична прогресия. Числото, което прибавяме към всеки член за да получим следващият се нарича разлика на аритметичната прогресия и обикновено означаваме с $d$. Други означения, които ползваме са $a_1$ - първият член на аритметичната прогресия, $a_n$ - $n$-тият член на аритметичната прогресия, $n$ - броят на членовете на аритметичната прогресия и накрая с $S_n$ ще означаваме сумата на аритметичната прогресия. Една безкрайна аритметична прогресия е определена (т.е. можем да намерим всичко за нея), ако знаем нейният първи член и разликата й. За да е определена една крайна аритметична прогресия освен нейната разлика и първи член трябва да знаем и броя на членовете й. Формулата за общият член на една аритметична прогресия има следният вид $a_n=a_1+(n-1)d$, а за сумата на първите $n$ члена имаме, че $S_n=\frac{a_1+a_n}{2}.n$. Във формулата за сумата м...