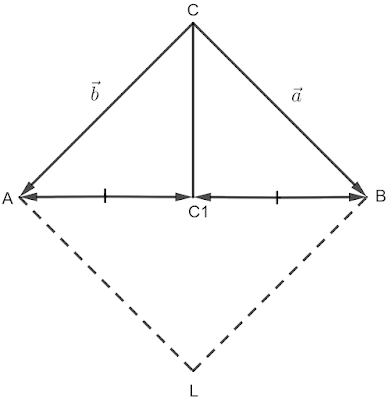
Средна отсечка в триъгълник 8 клас

Опредeление 1: Отсечка, която съединява средите на две от страните на триъгълник, ще наричаме средна отсечка в триъгълника. В даденият по-горе чертеж, отсечката $MN$ е средна отсечка, защото тя съединява две от средите на страните на $\triangle ABC$, а именно точките $M$ и $N$, които са среди съответно на $AC$ и $BC$. В сила са следните две важни теореми, които ще използваме при решаването на задачи: Теорема 1: Ако права минава през средата на една от страните на триъгълник и е успоредна на друга негова страна, то тя разполовява третата му страна. Казано с други думи, ако знаме, че една права минава през средата на една от страните на триъгълника и знаем също така, че е успоредна на друга негова страна, то със сигурност тази права ще мине през средата на третата страна т.е. тази права носи средната отсечка в триъгълника. Теорема 2: Всяка средна отсечка в триъгълник е успоредна на една от страните му и е равна на половината от нея. От тази теорема, можем да запишем някои важни фак...