Булеви функции - основни понятия и дефиниции - част I

Определение 1: Нека $B_2=\{0,1\}$. Булева (двоична) функция се нарича функция от вида $f:B_{2}^{n}\rightarrow B_{2}$, където $n\in\mathbb{Z^{+}}$.

В случая множеството $B_{2}^{n}=B_2\times B_2\times B_2\times\ldots\times B_2$ се състои от всички наредени $n$-торки от нули и единици. Очевидно множеството $B_{2}^{n}$ e крайно и функцията $f:B_{2}^{n}\rightarrow B_{2}$ съпоставя на всяка двоична $n$-торка $(x_1, x_2,\ldots, x_n)$ стойности $\{0,1\}$. Функцията $f$ е функция на $n$ независими променливи, като тези променливи взимат стойности $\{0,1\}$.

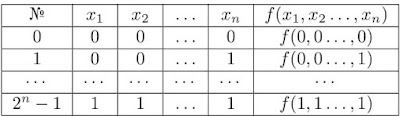
Всяка двоична функция можем да представим със следната таблица:

Всички двоични функции също могат да бъдат представени със следната таблица:

Множеството на всички двоични функции на $n$ променливи ще означаваме с $F_2$.

Теорема 1: Броят на двоичните функции на $n$ променливи е $|F_2|=2^{2^n}$.

Нека да конструираме в таблица всички двоични функции на една променлива:

Функциите $f_0(x)=0$ и $f_3(x)=1$ се наричат константи, функцията $f_1(x)=x$ се нарича идентитет, а функцията $f_2(x)=\overline{\rm x}$ се нарича отрицание на $x$.

Нека сега конструираме в таблица всички възможни двоични функции на две променливи:

Ще използваме следният запис на основните булеви функции, вместо да записваме $f(x_1,x_2)$ ще пишем $x_1fx_2$, например вместо $\lor(x_1,x_2)$ ще пишем $x_1\lor x_2$.

Сега нека кажем наименованията на основните булеви функции на две променливи:

1. Функциите $f_0(x_1,x_2)=0$ и $f_{15}(x_1,x_2)=1$ се наричат съответно, "константата $0$" и "константата $1$", за по-кратко, ще ги бележим с "$\bf{0}$" и "$\bf{1}$".
2. Функцията $f_1(x_1,x_2)$ се нарича "конюнкция" или още "логическо и", ще я бележим с "$\bf{.}$", в литературата още се среща и означението "$\bf{\land}$".
3. Функциите $f_3(x_1,x_2)$ и $f_5(x_1,x_2)$ се наричат "идентитет" и за по-кратко ще бележим съответно $f_3(x_1,x_2)$ с "$\bf{x_1}$", а $f_5(x_1,x_2)$ с "$\bf{x_2}$".
4. Функцията $f_6(x_1,x_2)$ се нарича "изключващо или" и за по-кратко ще бележим с "$\bf{+}$".
5. Функцията $f_7(x_1,x_2)$ се нарича $дизюнкция$ или още "логическо или" и ще бележим с "$\bf{\lor}$".
6. Функцията $f_8(x_1,x_2)$ се нарича "Стрелка на Пиърс" и ще я бележим с "$\bf{\downarrow}$".
7.  Функцията $f_9(x_1,x_2)$ се нарича "еквивалентност" и ще я бележим с "$\bf{\equiv}$" в различни източници функцията още се отбелязва и със символите $\bf{\iff}$ и "$\bf{\leftrightarrow}$".
8. Функцията $f_{10}(x_1,x_2)$ се нарича "отрицанието на $x_2$" и ще я бележим с "$\bf{\overline{\rm x_2}}$".
9. Функцията $f_{12}(x_1,x_2)$ се нарича "отрицанието на $x_1$" и ще я бележим с "$\bf{\overline{\rm x_1}}$".
10. Функцията $f_{13}(x_1,x_2)$ се нарича "импликация" ("следва") и ще я бележим с "$\bf{\rightarrow}$".
11. Функцията $f_{14}(x_1,x_2)$ се нарича "Черта на Шефер" и ще я бележим с $\bf{\mid}$.

Броят на всички булеви функции на две променливи е $16$, т.е. $|F_2|=16$. С нарастването на броят на аргументите, броят на булевите функции расте много бързо. 

1 Задача: Да се пресметне $x_1.0$.

Решение: Нека разгледаме следната таблица на истинност:

 

Тъй като, $0.0=0$ (виж конюнкцията - $f_1(x_1,x_2)$ какви стойности приема при $x_1=0$ и $x_2=0$ от таблицата на всички двоични функции на две променливи) и $1.0=0$ (виж конюнкцията - $f_1(x_1,x_2)$ какви стойности приема при $x_1=1$ и $x_2=0$ от таблицата на всички двоични функции на две променливи), следователно $x_1.0=0$.

2 Задача: Да се пресметне $x_1+x_2$.

Решение: Нека разгледаме следната таблица на истинност:

Тъй като, $0+0=0$ (виж изключващото или - $f_6(x_1,x_2)$ какви стойности приема при $x_1=0$ и $x_2=0$ от таблицата на всички двоични функции на две променливи) и $1+1=0$ (виж изключващото или - $f_6(x_1,x_2)$ какви стойности приема при $x_1=1$ и $x_2=1$ от таблицата на всички двоични функции на две променливи), следователно $x_1+x_1=0$.

3 Задача: Да се пресметне $x_1+1$.

Решение: Нека разгледаме следната таблица на истинност:

Тъй като, $0+1=1$ (виж изключващото или - $f_6(x_1,x_2)$ какви стойности приема при $x_1=0$ и $x_2=1$ от таблицата на всички двоични функции на две променливи) и $1+1=0$ (виж изключващото или - $f_6(x_1,x_2)$ какви стойности приема при $x_1=1$ и $x_2=1$ от таблицата на всички двоични функции на две променливи), следователно $x_1+1=\overline{\rm x_1}$.

4 Задача: Да се пресметне $x_1\lor 1$.

Решение: Нека разгледаме следната таблица на истинност:

Тъй като, $0\lor 1=1$ (виж дизюнкцията - $f_7(x_1,x_2)$ какви стойности приема при $x_1=0$ и $x_2=1$ от таблицата на всички двоични функции на две променливи) и $1\lor 1=1$ (виж изключващото или - $f_7(x_1,x_2)$ какви стойности приема при $x_1=1$ и $x_2=1$ от таблицата на всички двоични функции на две променливи), следователно $x_1\lor 1=1$.

Теорема 1 (Закони на Де Морган) В сила са равенствата $\overline{\rm x_1.x_2}=\overline{\rm x_1}\lor \overline{\rm x_2}=x_1\mid x_2$ и $\overline{\rm x_1\lor x_2}=\overline{\rm x_1}. \overline{\rm x_2}=x_1\downarrow x_2$.

Доказателство: Ще докажем теоремата на Де Морган като построим следната таблица на истинност:

От нея ясно се вижда, че равенствата, които трябваше да докажем са изпълнени, с което и теоремата на Де Морган е доказана.

Задачи за самостоятелно работа:

1. Да се пресметне $x_1\lor 0$.

2. Да се пресметне $x_1+\overline{\rm x_1}$.

3. Да се пресметне $x_1\lor\overline{\rm x_1}$.

4. Да се пресметне $x_1\lor x_1$.

5. Да се пресметне $x_1.\overline{\rm x_1}$.

Използвана литература:

1. Дискретна математика, Светла Бойчева, Стефка Толева-Стоименова, изд. Сиела 2018 г.

2. Увод в дискретната математика, Красимир Манев, изд. КЛМН 2012 г.

3. Въведение в дискретната математика, Христо Кискинов, Пловдивско университетско издателство