Събиране и изваждане на вектори 8 клас

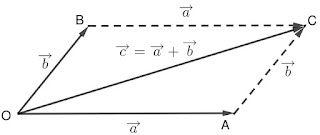
Нека имаме векторите $\overrightarrow{a}$ и $\overrightarrow{b}$ и точка $O$ е някаква произволна точка от равнината. Тогава, ако вземем векторите $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{AB}=\overrightarrow{b}$, то векторът $\overrightarrow{c}$ се нарича сбор или още сума на векторите $\overrightarrow{a}$ и $\overrightarrow{b}$.

Това правило за построяването на сбора (сумата) на два вектора, които не лежат на една права или на успоредни прави (т.е. да не са колинеарни) ще наричаме правило на триъгълника.

Сега да разгледаме още едно правило за събиране на вектори а именно правилото на успоредника:

Нека отново $\overrightarrow{a}$ и $\overrightarrow{b}$ са два вектора, които не лежат на една и съща права или на успоредни прави (т.е. не са колинеарни). Нека освен това да изберем една произволна точка $O$ в равнината. Построяваме векторите $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Сега допълваме до успоредник, т.е. построяваме векторите $\overrightarrow{BC}=\overrightarrow{a}$ и $\overrightarrow{AC}=\overrightarrow{b}$. Векторът $\rightarrow{OC}=\overrightarrow{c}$ е сборът на векторите $\overrightarrow{a}$ и $\overrightarrow{b}$ по правилото на успоредника

Нека сега кажем и някои свойства на сбора на вектори:

1. $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$;

2.$(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})$;

3. $\overrightarrow{a}+(-\overrightarrow{a})=\overrightarrow{0}$

4. $\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}$.

Можем да кажем, че разликата на векторите $\overrightarrow{a}$ и $\overrightarrow{b}$ т.е. $\overrightarrow{a}-\overrightarrow{b}$ е равна на векторът $\rightarrow{a}+(-\overrightarrow{b})$.

Често когато решаваме задачи и търсим разликата на два вектора с общо начало е удобно да запомним формулата $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$.

1 Задача Даден е успоредникът $ABCD$. Да се намери : 

а) $\overrightarrow{AB}+\overrightarrow{BC}$; 

б) $\overrightarrow{AB}+\overrightarrow{AD}$.

Решение:

а) 

Трябва да намерим сборът на векторите $\overrightarrow{AB}=\overrightarrow{a}$ и $\overrightarrow{BC}=\overrightarrow{b}$. Както е видно от направеният чертеж краят на векторът $\overrightarrow{a}$ съвпада с началото на векторът $\overrightarrow{b}$, следователно за да съберем тези два вектора трябва да приложим правилото на триъгълника, от където намираме, че $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}$ т. е. $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$. 

б)

Тъй като векторите $\overrightarrow{AB}$ и $\overrightarrow{AD}$ имат общо начало точката $A$ за да намерим сборът им $\overrightarrow{AB}+\overrightarrow{AD}$ е необходимо да приложим правилото на успоредника. Така получаваме, че $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}$, т.е. $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.

2 Задача Даден е триъгълникът $ABC$. Намерете $\overrightarrow{AB}-\overrightarrow{AC}$

Решение:

Тъй като векторите $\overrightarrow{AB}$ и $\overrightarrow{AC}$ построяваме векторите $\overrightarrow{CD}=\overrightarrow{AB}=\overrightarrow{a}$ и $\overrightarrow{BD}=\overrightarrow{AC}=\overrightarrow{b}$, т.е. допълваме триъгълникът $ABC$ до успоредник. Видяхме, при правилото на успоредника, че $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$. Така в случая на тази задача получаваме, че $\overrightarrow{CB}=\overrightarrow{a}-\overrightarrow{b}$ с което задачата е решена. 

3 Задача За триъгълникът $ABC$ намерете $\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}$.

Решение:

Тъй като за векторите $\overrightarrow{BC}$ и $\overrightarrow{CA}$, краят на единия и началото на другия съвпадат, прилагаме правилото на триъгълника за събиране на два вектора, от където имаме, че $\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{BA}$. Сега търсим сборът на векторите $\overrightarrow{BA}+\overrightarrow{AB}$. Знаем, че $\overrightarrow{BA}=-\overrightarrow{AB}$, от където имаме, че $\overrightarrow{BA}+(-\overrightarrow{BA})$. Сега като приложим следното свойство на сбора на вектори $\overrightarrow{a}+(-\overrightarrow{a})=\overrightarrow{0}$ получаваме, че $\overrightarrow{BA}+(-\overrightarrow{BA})=\overrightarrow{0}$, т.е. $\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{0}$, с което задачата е решена.

4 Задача Точката $P$ е средата на страната $AC$ на триъгълника $ABC$. Намерете сбора $\overrightarrow{BP}+\overrightarrow{CP}$.

Решение:

От това, че точката $P$ е среда на $CA$ следва, че $\overrightarrow{CP}=\overrightarrow{PA}$. От правилото на триъгълника имаме, че $\overrightarrow{BP}+\overrightarrow{PA}=\overrightarrow{BA}$ с което задачата е решена.

Задачи за самостоятелна работа:

1. За успоредника $ABCD$ намерете $\overrightarrow{AB}+\overrightarrow{BD}$.

2. Даден е успоредникът $ABCD$. Точката $O$ е пресечна точка на диагоналите му. През $O$ е построена права, която пресича страните на успоредника $AB$ и $CD$ съответно в точките $K$ и $M$. Да се намери:

а) $\overrightarrow{OB}-\overrightarrow{OK}$;  б) $\overrightarrow{AB}-\overrightarrow{DM}$; в) $\overrightarrow{AK}-\overrightarrow{CM}$; г) $\overrightarrow{CK}-\overrightarrow{CM}$; д) $\overrightarrow{MB}-\overrightarrow{DK}$.

3. Да се докаже, че за всеки успоредник $ABCD$ и произволна точка $O$ е изпълнено равенството $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}$.

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу: