Успоредник 7 клас

Успоредник - дефиниции, свойства и задачи

Определение 1: Четириъгълник, на който двойките срещуположни страни са успоредни, се нарича успоредник.

Признаци за успоредник

Теорема 1 (признак): Четириъгълник, на който срещуположните страни са равни, е успоредник.

Теорема 2 (признак): Четириъгълник, на който една двойка срещуположни страни са успоредни и равни, е успоредник.

Теорема 3 (признак): Четириъгълник, на който диагоналите взаимно се разполовяват, е успоредник.

Свойства на успоредника

Теорема 4 (свойство): В успоредника двойките срещуположни страни са равни.

Следствие 1: В успоредника срещуположните ъгли са равни.

Следствие 2: В успоредника сборът на прилежащите на коя да е страна ъгли е $180^{\circ}$.

Доказателство: Нека ABCD е успоредник. Тъй като AB ∥ CD и AD е секуща, то $\sphericalangle A + \sphericalangle D = 180^{\circ}$ (като едностранни ъгли). Аналогично за другите двойки прилежащи ъгли.

Теорема 5 (свойство): В успоредника диагоналите взаимно се разполовяват.

Решени задачи

Задача 1: Да се намерят ъглите на успоредник, ако ъгълът между височините му през върха на един от неговите остри ъгли е $140^{\circ}$.

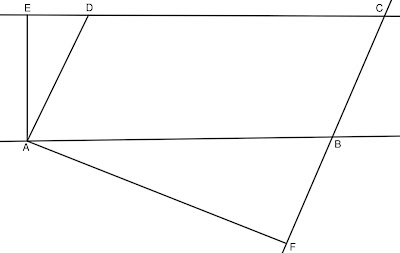
Решение: Нека $AE$ и $AF$ са височините съответно към страните $CD$ и $BC$. Нека $\sphericalangle DAB = \alpha$, следователно от Следствие 2 имаме, че $\sphericalangle ABC = 180^{\circ} - \alpha$. Освен това ъглите $ABC$ и $ABF$ са съседни, откъдето $\sphericalangle ABF = \alpha$ и $\sphericalangle FAB = 90^{\circ} - \alpha$ (в правоъгълния $\triangle BFA$).

От друга страна $\sphericalangle BAD = \sphericalangle ADE = \alpha$ (кръстни ъгли), а $\sphericalangle DAE = 90^{\circ} - \alpha$ (в правоъгълния $\triangle DAE$).

Ъгълът между височините е $\sphericalangle EAF = 140^{\circ}$ по условие. Имаме: $$90^{\circ} - \alpha + \alpha + 90^{\circ} - \alpha = 140^{\circ}$$ $$180^{\circ} - \alpha = 140^{\circ}$$ $$\alpha = 40^{\circ}$$ Следователно $\sphericalangle BAD = \sphericalangle DCB = 40^{\circ}$ и $\sphericalangle ADC = \sphericalangle ABC = 140^{\circ}$.

Задача 2: Периметърът на успоредника $ABCD$ е равен на $60$ cm. Ъглополовящите на ъглите $A$ и $B$ пресичат страната $CD$ съответно в точките $M$ и $N$. Намерете страните на успоредника, ако $MN=3$ cm.

Решение: Нека $\sphericalangle DAM = \sphericalangle MAB = \alpha$, $\sphericalangle ABN = \sphericalangle CBN = \beta$, $AB = CD = a$ и $AD = BC = b$.

От $AB \parallel CD$ следва, че $\sphericalangle BAM = \sphericalangle AMD$ (кръстни ъгли), следователно $\triangle AMD$ е равнобедрен и $AD = DM = b$. Аналогично $\triangle BCN$ е равнобедрен и $BC = CN = b$.

Имаме $CD = DM + MN + NC = b + 3 + b = 2b + 3 = a$.

За периметъра: $P = 2(a + b) = 60 \Rightarrow a + b = 30$

Заместваме $a = 2b + 3$: $$2b + 3 + b = 30$$ $$3b = 27$$ $$b = 9 \text{ cm}$$ $$a = 2 \cdot 9 + 3 = 21 \text{ cm}$$

Задачи за самостоятелна работа

1. В успоредника $ABCD$ ъглополовящите на ъглите $A$ и $B$ се пресичат в точка $M$ от страната $CD$. Докажете, че $M$ е среда на $CD$ и $AB=2AD$.

2. Нека $M$ и $N$ са средите съответно на страните $AB$ и $CD$ на успоредника $ABCD$. Докажете, че четириъгълниците $AMND$ и $MBCN$ са успоредници.

3. Докажете, че ако диагоналът $AC$ в успоредника $ABCD$ е ъглополовяща на ъгъл $A$, то диагоналът $BD$ е перпендикулярен на $AC$.

4. Докажете, че ако един четириъгълник има двойка успоредни страни и двойка равни срещуположни ъгли, той е успоредник.

5. Нека $K$ е пресечната точка на ъглополовящите на $\sphericalangle BAD$ и $\sphericalangle ADC$ на успоредника $ABCD$. Докажете, че $\sphericalangle AKD=90^{\circ}$.

Видео уроци

Още обяснени и решени задачи свързани с успоредници можете да намерите в клипа ми:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +