Триъгълник. Сбор на ъгли в триъгълник. Външен ъгъл на триъгълник 7 клас

В настоящият урок ще научим на колко е равен сборът от ъглите в произволен триъгълник, какво е външен ъгъл на триъгълник, на колко е равен сборът от външните ъгли в триъгълника, както и ще решим някои задачи.

Теорема 1: Сборът от ъглите на всеки триъгълник е равен на \(180^{\circ}\) или \(\alpha+\beta+\gamma=180^{\circ}\).

Като следствие от тази теорема, можем да кажем, че всеки триъгълник има най-много един тъп ъгъл, както и, че сборът от острите ъгли в правоъгълен триъгълник е равен на \(90^{\circ}\).

Определение 1: Външен ъгъл на триъгълник се нарича ъгъл, съседен на вътрешен ъгъл на триъгълник (в случая на чертежа външните ъгли са съответно \(\alpha^{\prime}, \beta^{\prime}, \gamma^{\prime}\)).

Теорема 2: Всеки вънжен ъгъл на триъгълник е равен на сбора от двата несъседни на него вътрешни ъгли на триъгълник.

Доказателство: За да унагледим доказателството ще използваме горният чертеж и разбира се Теорема 1. Тъй като \(\alpha+\beta+\gamma=180^{\circ}\) имаме, че \(\alpha=180^{\circ}-\beta-\gamma=180^{\circ}-(\beta+\gamma)\). От друга страна \(\alpha\) и \(\alpha^{\prime}\) са съседни ъгли и следователно \(\alpha+\alpha^{\prime}=180^{\circ}\). Сега, нека в последното равенство заменим \(\alpha\) с равното му \(180^{\circ}-(\beta+\gamma)\) и получаваме \(180^{\circ}-(\beta+\gamma)+\alpha^{\prime}=180^{\circ}\), от където \(\alpha^{\prime}=\beta+\gamma\). Доказателството на останалите две равенства е абсолютно аналогично.

Като следствие от Теорема 2 можем да кажем, че всеки вънжен ъгъл на триъгълник е по-голям от всеки вътрешен, несъседен нему ъгъл на триъгълника.

Решени задачи

1 Задача: Намерете ъглите \(\alpha\), \(\beta\) и \(\gamma\) на \(\triangle ABC\), ако \(\alpha:\beta:\gamma=2:5:3\).

Решение: Нека \(\alpha=2x\), \(\beta=5x\) и \(\gamma=3x\), тогава от Теорема 1 имаме, че \(2x+5x+3x=180^{\circ}\) и следователно \(x=18^{\circ}\). Сега вече можем да намерим ъглите \(\alpha=2\cdot18^{\circ}=36^{\circ}\), \(\beta=5\cdot18^{\circ}=90^{\circ}\) и \(\gamma=3\cdot18^{\circ}=54^{\circ}\).

2 Задача: Докажете, че сборът от външните ъгли на всеки триъгълник е равен на \(360^{\circ}\).

Решение: Нека разгледаме сборът \(\alpha^{\prime}+\beta^{\prime}+\gamma^{\prime}\). От Теорема 2 имаме, че \(\alpha^{\prime}=\beta+\gamma\), \(\beta^{\prime}=\alpha+\gamma\) и \(\gamma^{\prime}=\alpha+\beta\). Нека сега в сборът \(\alpha^{\prime}+\beta^{\prime}+\gamma^{\prime}\) заменим всяко едно от събираемите съответно с техните равни т.е \(\alpha^{\prime}\) с \(\beta+\gamma\), \(\beta^{\prime}\) с \(\alpha+\gamma\) и \(\gamma^{\prime}\) с \(\alpha+\beta\). Така получаваме равенството \(\alpha^{\prime}+\beta^{\prime}+\gamma^{\prime}=\beta+\gamma+\alpha+\gamma+\alpha+\beta\), от където \(\alpha^{\prime}+\beta^{\prime}+\gamma^{\prime}=2(\alpha+\beta+\gamma)\) и тъй като \(\alpha+\beta+\gamma=180^{\circ}\) следва, че \(\alpha^{\prime}+\beta^{\prime}+\gamma^{\prime}=360^{\circ}\) и задачата е решена.

3 Задача: Ъглополовящите \(AA_1\) и \(BB_1\) на \(\triangle ABC\) се пресичат в точката \(O\). Намерете \(\gamma\), ако \(\sphericalangle AOB=125^{\circ}\).

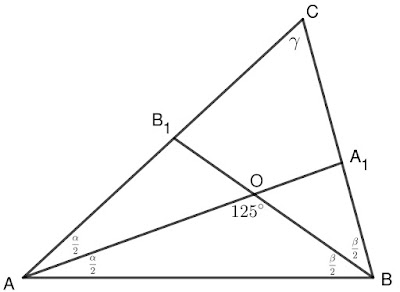
Решение: Ще използваме стандартните означения за ъглите в \(\triangle ABC\). Тъй като \(AA_1\) и \(BB_1\) са ъглополовящи следва, че \(\sphericalangle CAA_1=\sphericalangle A_1AB=\frac{\alpha}{2}\) и \(\sphericalangle CBB_1=\sphericalangle B_1BA=\frac{\beta}{2}\). Според Теорема 1 за триъгълника \(AOB\) имаме, че \(\frac{\alpha}{2}+\frac{\beta}{2}+\sphericalangle AOB=180^{\circ}\), следователно \(\frac{\alpha}{2}+\frac{\beta}{2}+125^{\circ}=180^{\circ}\), от където намираме, че \(\frac{\alpha}{2}+\frac{\beta}{2}=55^{\circ}\). Нека запишем \(\frac{\alpha}{2}+\frac{\beta}{2}=55^{\circ}\) във вида \(\frac{\alpha+\beta}{2}=55^{\circ}\). Така получаваме, че \(\alpha+\beta=110^{\circ}\). Сега прилагаме Теорема 1 за \(\triangle ABC\) и имаме, че \(\alpha+\beta+\gamma=180^{\circ}\). Ние вече получихме, че \(\alpha+\beta=110^{\circ}\) и следователно \(110^{\circ}+\gamma=180^{\circ}\) и \(\gamma=70^{\circ}\) с което задачата е решена.

Задачи за самостоятелна работа

1. Намерете мерките на ъглите в един триъгълник, ако те се отнасят както числата \(4:3:2\).

2. Даден е \(\triangle ABC\) с \(\sphericalangle CAB=65^{\circ}\) и \(\sphericalangle ABC=73^{\circ}\). Ъглополовящата \(CD\) на \(\sphericalangle BCA\) \((D\in AB)\) разделя дадения триъгълник на други два триъгълника - \(\triangle ADC\) и \(\triangle BDC\). Намерете ъглите на тези триъгълници.

3. Ако мерките на външните ъгли на триъгълник се отнасят както \(4:3:5\), намерете вътрешните му ъгли.

4. В триъгълник един от вътрешните му ъгли е \(40^{\circ}\), а един външен ъгъл е \(30^{\circ}\). Намерете ъглите на този триъгълник.

5. В триъгълника \(ABC\) е известно, че \(\sphericalangle A\) е с 10% по-голям от \(\sphericalangle B\) и тъпият ъгъл между ъглополовящите \(AL\) и \(CN\) е равен на \(115^{\circ}\). Да се намери \(\sphericalangle C\).

Видео уроци:

Още обяснени и решени задачи свързани с този урок можете да намерите в клипа ми даден по-долу:

Използвана литература:

1. Сборник за 7 клас, Пенка Рангелова, Константин Бекриев, Лилия Дилкина, Нина Иванова изд. Коала Прес, Пловдив, 2020

2. Тест Математика 7 клас, Донка Гълъбова, Адриана Хаджийска, Анна Аначкова и др., изд. Веди, София, 2020

3. Сборник задачи по математика за 7 клас, Мария Лилкова, Пенка Нинова, Таня Стоева и др., изд. Просвета, София

4. Книга за ученика за 7 клас, Здравка Паскалева, Мая Алашка, Райна Алашка, изд. Архимед, София, 2018

5. Текуща подготовка по математика за националното външно оценяване в 7 клас, Боянка Савова, Мария Тодорова, Веселин Златилов, изд. Просвета, София, 2020

6. Нови пробни изпити за външно оценяване и кандидатстване след 7 клас, изд. Регалия 6, София 2015

7. Тестове по математика, Любомир Любенов, Цеца Байчева, изд. DOMINO, 2017

8. Нови тематични и общи тестове по математика за 7 клас, Марина Рангелова, изд. Коала Прес, 2008

9. Учебно помагало за задължително избираема подготовка по математика за 7 клас, Иван Тонов, Таня Тонова, изд. Просвета, София, 2011

10. Тестове по математика за 7 клас, Лилия Дилкина, Константин Бекриев, изд. Коала Прес, Пловдив, 2014

11. Сборник контролни работи и тестове по математика 7 клас, Пенка Рангелова, изд. Коала Прес, Пловдив, 2009

12. Сп. Математика

13. Сп. Математика +